Spis treści
- Wstęp / wprowadzenie - metody rozwiązywania
- Cel projektu
- Realizacja projektu
- Instrukcja dla użytkownika
- Użyte instrukcje
- Podsumowanie
- Bibliografia
Ad.1
Sudoku – łamigłówka, której celem jest wypełnienie diagramu 9 x 9 w taki sposób, aby w każdym wierszu, w każdej kolumnie i w każdym z dziewięciu pogrubionych kwadratów 3 x 3 (zwanych „regionami”) znalazło się po jednej cyfrze od 1 do 9. (Uwaga! Dla łamigłówki 6x6 region jest prostokątem o wymiarach 2x3 kratki)
Zasady przypominają trochę kwadrat łaciński, wymyślony i badany przez średniowiecznych matematyków z terenów Arabii (XIII wiek). W Sudoku, w przeciwieństwie do kwadratu łacińskiego, cyfry nie mogą się powtarzać nie tylko w żadnym wierszu i kolumnie, ale także w regionie 3 x 3.
Metoda 1
Polega na znajdowaniu miejsca, gdzie w obrębie regionu 3 x 3 pasuje dana cyfra na zasadzie eliminacji rzędów i kolumn, w których ta cyfra znajduje się w innych kwadratach.
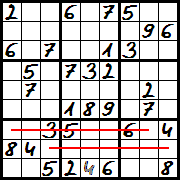
Diagram 1 – cyfrę 4 wpisać można tylko w jedno pole środkowego dolnego kwadratu (oba pozostałe rzędy są już zajęte).
Diagram 2 – bardziej skomplikowany przypadek, znalezienie miejsca dla cyfry 3. Cyfra 3 pasuje w dwa miejsca w środkowym dolnym kwadracie. Pozwala to na wyeliminowanie tego rzędu (cyfra 3 musi znaleźć się w tym rzędzie, niezależnie, czy na polu po lewej czy po prawej), więc w prawym dolnym kwadracie dwa rzędy są zajęte. Jedną kolumnę zajmuje wpisana już cyfra 3, więc pozostaje jedyne pole, gdzie można wpisać cyfrę 3.(to obok 8)
1.  2. 2. 
Metoda 2
Polega na dopełnianiu rzędu, kolumny lub kwadratu 3 x 3 cyframi od 1 do 9.
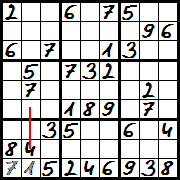
Diagram 3 – w dolnym rzędzie brakuje już tylko dwóch cyfr, Łatwo sprawdzić, że są to 1 i 7. Do drugiego pustego pola od lewej pasuje tylko cyfra 1, ponieważ w tej kolumnie już znajduje się cyfra 7. Cyfra 7 natomiast powinna się znaleźć w pierwszym pustym polu po lewej.
Diagram 4 – w pewnym momencie można dopełnić cały kwadrat, dla przykładu lewy dolny. Cyfra 2 pasuje tylko do środkowej kolumny, cyfra 6 tylko do środkowego rzędu. Do tego, gdzie umiejscowić cyfrę 9, można w tym przypadku dojść na dwa sposoby :
- bo jest to ostatnia cyfra, jaka pozostała do wpisania w tym kwadracie,
- bo nie można tam wpisać ani cyfry 2, ani cyfry 6.
3.  4. 4. 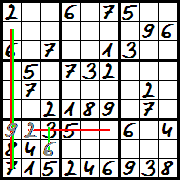
Metoda 3
Jest to metoda wymagająca „bazgrania” po diagramie. Polega ona na stawianiu w odpowiednim miejscu kratki kropek-podpowiedzi. Kropki stawia się tak, by jasno określić cyfrę – patrz Diagram 5.
5. 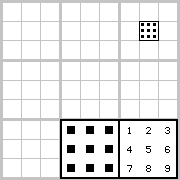
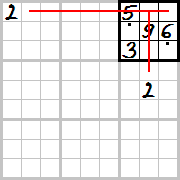
Diagram 6 – rozwiązując Sudoku, często spotykamy się z sytuacją, kiedy w kwadracie 3 × 3 dana cyfra może znaleźć się dokładnie w dwóch miejscach. Zaznaczamy wtedy oba te miejsca kropką, postawioną w odpowiednim punkcie kratki.
Diagram 7 i 8 – kiedy później, w trakcie rozwiązywania, jedno z tych miejsc zostanie zapełnione jakąś cyfrą inną niż wskazuje kropka, to w drugie miejsce można automatycznie wpisać cyfrę wskazaną przez kropkę.
6.  7. 7. 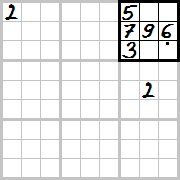 8. 8. 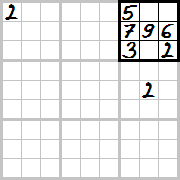
Ad 2
Cele projektu :
Utworzenie programu do rozwiązywania łamigłówki SUDOKU na podstawie znanych, wprowadzonych przez użytkownika liczb. Program potrafi rozwiązywać różne warianty łamigłówki różniące się rozmiarami planszy: 6x6, 9x9, 16x16, 25x25 oraz sudoku nieregularne 9x9. Poniższy opis odnosi się do klasycznego rozmiaru planszy czyli 9 x 9. Dla pozostałych rozmiarów opis jest analogiczny.
Ad.3
Realizacja projektu :
Program został utworzony w popularnym języku skryptowym PHP. Grafika jest składana przy wykorzystaniu kodu HTML wraz z CSS bez użycia biblioteki PHP GD. Dzięki temu możliwe jest korzystanie z programu bez względu na środowisko graficzne i system operacyjny. Wystarczy dostęp do internetu poprzez przeglądarkę. W przypadku braku dostępu do internetu należy zainstalować serwer z obsługą PHP na lokalnym komputerze. Wybór wolnego, skryptowego języka niesie za sobą pewne ograniczenia. Jest wielce prawdopodobne, że dla planszy o rozmiarze 25x25 zostanie przekroczony domyślny czas przeznaczony na działanie skryptu. Dotyczy to zwłaszcza sytuacji, w których użytkownik wprowadził niewielką ilość liczb.
Opis algorytmu rozwiązującego łamigłówkę :
Wszystkie puste pola są kolejno ustawiane w szereg i wpisane do tablicy $ptab. Wraz z numerem pola zapamiętywane jest jego położenie na planszy (X,Y) oraz numer regionu na którym leży. W nieskończonej pętli sprawdzane są kolejne liczby z powyższej tablicy, gdy żadna liczba nie pasuje, następuje cofnięcie do poprzedniej liczby. Sprawdzenie, czy badana liczba pasuje w danym miejscu następuje przy wykorzystaniu tablic $xtab, $ytab, $rtab $ltab, które zawierają liczby z bitowym zapisem informacji o sytuacji na planszy -
$ltab - tablica liczb, których kolejne bity informują, które pola wypełnił użytkownik - jedna liczba oznacza jeden wiersz
$xtab - tablica liczb, których kolejne bity informują, które liczby wykorzystał użytkownik - jedna liczba oznacza jedną kolumnę
$ytab - tablica liczb, których kolejne bity informują, które liczby wykorzystał użytkownik - jedna liczba oznacza jeden wiersz
$rtab - tablica liczb, których kolejne bity informują, które liczby wykorzystał użytkownik - jedna liczba oznacza jeden region
Ad. 4
Reguły jakie musi spełniać poprawnie wypełniona plansza :
• Cyfry w obrębie każdego kwadratu 3x3 nie mogą się powtarzać
• Cyfry w obrębie każdej kolumnie 1x9 nie mogą się powtarzać
• Cyfry w obrębie każdego rzędu 9x1 nie mogą się powtarzać
Z tych reguł wynikają kolejne, które mogą pomóc w rozwiązaniu planszy :
• W każdym kwadracie 3x3 znajdują się wszystkie cyfry 1-9
• W każdej kolumnie 1x9 znajdują się wszystkie cyfry 1-9
• W każdym rzędzie 9x1 znajdują się wszystkie cyfry 1-9
Ad.5
Zaimplementowana funkcjonalność :
program automatycznie sprawdza czy użytkownik poprawnie wprowadził liczby tzn czy istnieje rozwiązanie. Jeżeli nie to wyświetla odpowiedni komunikat i umożliwia dokonanie poprawek. Możliwe komunikaty dotyczą dwóch liczb w tym samym wierszu, kolumnie, regionie lub braku rozwiązań.
Program nie sprawdza czy układ ma wiele rozwiązań – wyświetla tylko pierwsze prawidłowe
Ad.6
Podsumowanie
Podczas generowania plansz sudoku należy pamiętać, że układ powinien posiadać dokładnie jedno rozwiązanie.
W klasycznym SUDOKU wypełnione pola są rozmieszczone symetrycznie względem środka planszy.
Ad. 7
Bibliografia
1. wikipedia.pl
2. sudoku.org.pl
3. math.uni.lodz.pl
|
 2.
2. 
 4.
4. 

 7.
7.  8.
8. 